Compression Spring Dynamic Load Impact
Compression Spring Design Resources – Spring Performance
When a compression spring is loaded, or unloaded, a surge wave is established that transmits torsional stress from the point of loading along the spring length to the point of restraint. The surge wave travels at a velocity approximately 1/10 of a normal torsional stress wave. Velocity of the torsional stress wave (VT) is given by:
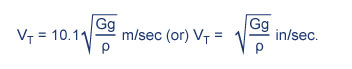
Velocity of the surge wave VS varies with material and compression spring design, but is usually in the range of 50 to 500 m/sec. The surge wave limits the rate at which a compression spring can absorb or release energy by limiting impact velocity V. Impact velocity is the spring velocity parallel to the spring axis and is a function of stress and material constants shown as:

This is a surprising result because impact velocity and stress are independent of the compression spring configuration. For steels, impact velocity is reduced to:

If a spring is compressed to a given stress level and released instantaneously, the maximum spring velocity is expressed as the stress divided by 35.5. Similarly, if a spring is loaded at a known velocity, instantaneous stress can be calculated. At very high loading velocities, instantaneous stress will exceed the stress calculated from the conventional static formula and will limit design performance. These equations for impact velocity are only concerned with the primary surge wave. Frequently, this wave will reflect from the other end of the compression spring, increasing stress. Compression springs loaded at high velocities are frequently subject to resonance phenomena.
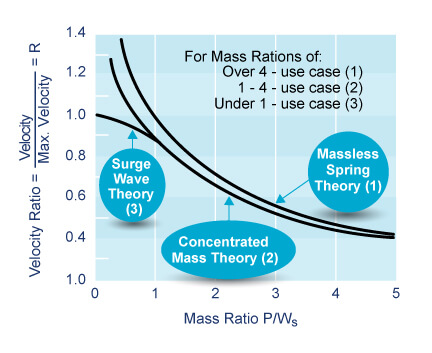
When the ration of the weight to be accelerated to the weight of the spring is less than 1, surge wave theory accurately predicts design performance. At high weight ratios and lower velocities, an energy balance is used to predict velocity of a weight projected from the spring end or deflection of the spring when impacted by a mass. Velocity and deflection are related as:
For horizontal loading:

For vertical loading:

W/g is the mass that is being accelerated or decelerated and V is the axial velocity of the spring. These equations assume that the compression spring is massless and should only be used when the spring mass is less than 1/4 of the mass to be accelerated.
When the ratio of compression spring load to weight is less than 4, the energy required to accelerate the spring itself becomes appreciable. By assuming that all mass of the compression spring is concentrated at the moving end, Equations 3 and 4 can be corrected by substituting (W + WS/3) for W where WS is the compression spring weight.
Content Copyright Spring Manufacturers Institute, Inc.
This information is attributed to, and provided courtesy of, the Spring Manufacturers Institute, Inc. (SMI). Newcomb Spring and SMI provide this as advisory information only, and disclaim any and all liability of any kind for the use, application or adaption of material published on this web site.