Squareness of Compression Springs
Compression Spring Design Resources – Spring Performance
Squareness of a compression spring refers to the perpendicularity of the spring to its own axis. A spring that is "square" will exert more uniform loads, which may be needed in critical applications. Springs with ground ends generally offer better squareness than those with closed only ends, especially springs with smaller indexes. Larger spring indexes (D/d) reduce the effect that grinding has on squareness. Springs that are closed only are generally not "as square" as springs with ground ends.
To measure the squareness of a compression spring it is necessary to place the spring on a flat plate with a post or back plate set at a 90-degree angle (see illustration). Keep the bottom coil of the spring against the vertical plate while the spring is sitting flat on the horizontal plate. Rotate the spring until the gap at the top of the spring is at its widest point and measure the gap. This should be done on both ends by turning the spring over and measuring again. Considering that 1 degree equates to a gap of .017453" per inch of distance from the horizontal plate, the squareness of the spring can be calculated using the following formula:
|
Squareness in Degrees =
Gap
(FL x .017453)
|
Generally Accepted Squareness of Springs with Ground Ends Are:
- 3 Degrees (commercial)
- 1-2 Degrees (precision)
Spring Index (D/d) and the number of active coils in the spring affect the free angle tolerance and should be considered during the design stage. It is always best to work with your spring maker during the early stage in order to achieve the best design for your application and determine spring squareness.
Please contact the Newcomb Spring facility nearest you for more information on compression spring squareness and other considerations of spring design.
Resource Illustration
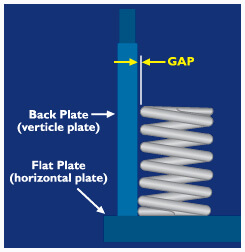
Squareness of a compression spring refers to the perpendicularity of the spring to its own axis.