Rectangular Wire Torsion Springs
Torsion Spring Design Resources – Rectangular Material
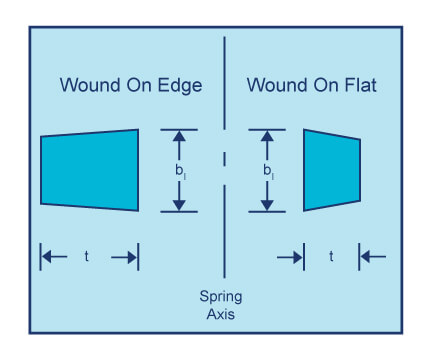
Rectangular-wire torsion springs have higher energy storage capacities than similar round-wire springs. The general comments on round-wire torsion springs apply to springs with rectangular wire. In producing springs from rectangular wire, the wire cross-section distorts and becomes "keystoned." The wire axial dimension b1 can be estimated from:
b1 = b ((C + 0.5) / C)
When axial length is critical, keystone-shaped wire can be purchased. This wire will have a near rectangular shape after coiling. The rate equation is:
R = M / Ɵ = Ebt3 / 6.6DNa
And the stress equation is:
S = (6M / bt2) KB
These equations are for torsion springs wound either on edge or on flat (shown in the diagram below). Stress correction factor KB is slightly lower than for round wire and can be approximated by:
KBID = 4C / (4C - 3)
KBOD = 4C / (4C + 3)
Sharp corners on rectangular wire cause stress concentrations and should be avoided, while generous corner radii of rolled wire reduce the wire cross sections sufficiently to lower the rate.
Content Copyright Spring Manufacturers Institute, Inc.
This information is attributed to, and provided courtesy of, the Spring Manufacturers Institute, Inc. (SMI). Newcomb Spring and SMI provide this as advisory information only, and disclaim any and all liability of any kind for the use, application or adaption of material published on this web site.
Resource Illustration
Sharp corners on rectangular wire cause stress concentrations and should be avoided, while generous corner radii of rolled wire reduce the wire cross sections sufficiently to lower the rate.