Compression Spring Dynamic Loading Resonance

---

Compression Spring Design Resources – Spring Performance

---

Resonance occurs in a compression spring when the frequency of the cyclic loading is near natural spring frequency or a multiple of it. Resonance can increase individual coil deflection and stress levels well above amounts predicted by static or equilibrium analysis. Resonance can also cause spring bounce, which results in loads considerably lower than calculated at the minimum spring deflection. To avoid compression spring loading resonance, natural spring frequency should be at least 13 times the operating frequency.

The natural frequency of a compression spring is inversely proportional to the time required for a surge wave to traverse the spring. For a compression spring without damping and with both ends fixed:

n = (1.2 x 10³d / (D₂N_a) √Gg / ρ; for steel n = (3.5 x 10⁵d / (D₂N_a) metric
(n is in hertz)

If a compression spring cannot be designed so the natural frequency is more than 13 times the operating frequency, or if the spring is to serve as a vibration damping device, it must utilize one of the several methods of energy absorption. Generally, these are friction devices in which the compression spring rubs against another element, such as a n internal damper coil, arbor, housing or another portion of the spring. Variable pitch springs and springs in combination are also occasionally used to avoid or minimize resonant frequency effects.

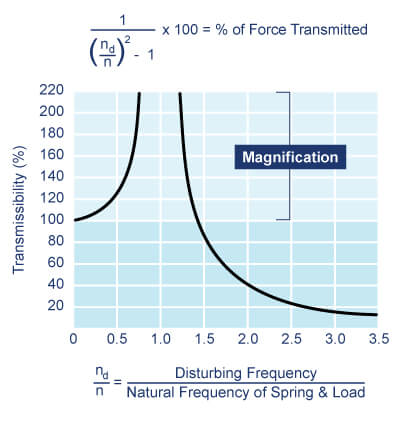
For vibration isolation system, the essential characteristic is that the natural frequency of the spring-mass system be as far as possible from the disturbing frequency. Filtering of disturbing forces may be calculated as:

% of force transmitted=1 / ((n_d / n)² - 1) x 100

where n_d is the frequency of the disturbing force and n the natural frequency of the spring-mass system.

If n_d/n is less than 1, the denominator in the percent of force transmitted equation should change to 1 - (n_d / n)². Note that the frequency n in this equation is the frequency of the spring-mass system and not the natural spring frequency. In fact, the most commonly used equation neglects the spring weight and is only defection dependent. The general equation is:

n = 15.8 / ∏ √gk / P metric (or) n = 1 / 2∏ √Gr / P

Content Copyright Spring Manufacturers Institute, Inc.

This information is attributed to, and provided courtesy of, the Spring Manufacturers Institute, Inc. (SMI). Newcomb Spring and SMI provide this as advisory information only, and disclaim any and all liability of any kind for the use, application or adaption of material published on this web site.

---